LOS MECANISMOS EN TECNOLOGIA
Vamos a hacer un estudio de todos los mecanismos uno a uno, viendo su uso y
los cálculos.
Pero primero empecemos por dejar claro que es eso de un mecanismo.
¿Qué son los Mecanismos?
Son elementos destinados a transmitir y/o transformar fuerzas y/o movimientos desde un elemento motriz (motor) a un elemento conducido (receptor), con la misión de permitir al ser humano realizar determinados trabajos con mayor comodidad y menor esfuerzo.

Existen 3 grupos principales de mecanismos:
1. Mecanismos de transmisión: se utilizan para modificar la fuerza de entrada por otra diferente de salida. Transmiten fuerzas de un sitio a otro.
2. Mecanismos de transformación: son aquellos en los que el elemento motriz y el conducido tienen distinto tipo de movimiento.
Transforman la velocidad de entrada en otra diferente de salida o transforman el movimiento de entrada en otro diferente de salida.
Por ejemplo un tornillo-tuerca, el tornillo gira y la tuerca se desplaza lineal o el sistema de poleas donde la velocidad de entrada se transforma en otra diferente de salida.
3. Otros Mecanismos: Aquí se agrupan todos los demás.
Tenemos mecanismos para regular el movimiento, por ejemplo los frenos, para acoplar o desacoplar ejes, por ejemplo los embragues y mecanismos que acumulan energía, por ejemplo los muelles.
Antes de empezar a estudiar los mecanismos tenemos que decir que la unidad correcta de la fuerza y el peso es el Newton.
Resulta que en la vida diaria nadie dice peso 40 Newtons, todo el mundo utiliza la unidad del Kilogramo, aunque estaría mal usada.
Como tecnología es un área sumamente práctica nosotros utilizaremos el Kg, aunque ya sabemos que físicamente es incorrecto.
Empecemos el estudio uno a uno.
MECANISMOS DE TRANSMISIÓN
LAS POLEAS
Se utilizan para subir o bajar cargas pesadas con menos esfuerzo.
- Polea Simple o Fija: es una rueda que tiene un ranura o acanaladura en su periferia, que gira alrededor de un eje que pasa por su centro.
Su fórmula es: Fuerza = Resistencia.
Resistencia es el peso que queremos subir con la polea y fuerza es el esfuerzo que tenemos que hacer para subir el peso.

Para levantar 20Kg necesitamos hacer una fuerza de 20Kg. La pregunta es…¿Cual es la ventaja?
Es más fácil levantar un peso tirando hacia arriba y además el peso de nuestro propio peso nos ayuda a levantar.
Si yo pesara 30Kg para levantar los 20Kg solo tendría que colgarme para subirlo.
- Polea móvil o compuesta: Es un conjunto de dos poleas, una de las cuales es fija, mientras que la otra es móvil.
La polea móvil dispone de un sistema armadura-gancho que le permite arrastrar la carga consigo al tirar de la cuerda.
Fórmula: Fuerza = Peso/2

En este tipo de poleas tenemos la ventaja de la polea fija y además la fuerza necesaria para levantar un peso es de la mitad.
- Polipasto: Este mecanismo está formado por grupos de poleas fijas y móviles.
Cuando tenemos más de una polea móvil le llamamos polipasto.
Por cada polea móvil siempre hay una fija; Número de poleas móviles = Numero de poleas fijas.
Su fórmula es: F = P/2n
Donde n es el número de poleas fijas o móviles que son siempre las mismas.

- Manivela Torno: Se trata de una barra acodada unida a un eje en el que se encuentra el torno que es un tambor alrededor del cual se enrolla una cuerda o cable para levantar un peso.
Su fórmula es: F x d = P x r
Donde d es la longitud de la barra y r el radio del tambor.

- Palanca o Balancin: es una barra rígida que oscila sobre un punto de apoyo debido a la acción de dos fuerzas contrapuestas, la fuerza o potencia y la resistencia.

Antes de seguir con los siguientes mecanismos te dejamos unos ejercicios para practicar los vistos hasta aquí.
1º) Escribe la fórmula de equilibrio de un balancín.
2º) Calcula la fuerza que se puede levantar con un balancín haciendo una fuerza de 40Kg sobre una barra de 10m, si la barra donde ponemos el peso es de 2m.
3º)a) Cuál es la fórmula de la polea simple?
b) Cuál es la ventaja de una polea simple?
4º) Calcula la fuerza necesaria para levantar un peso de 70Kg con una polea móvil.
5º) ¿Qué fuerza necesitamos para levantar 2000Kg con un polipasto de 3 poleas móviles?
6º) Para levantar un peso de 2000Kg con un mecanismo de manivela-torno que tiene una barra de 50cm, en un tambor de 30cm de radio. ¿Qué fuerza necesitaríamos hacer?
7º) Quiero levantar un peso de 600Kg haciendo una fuerza de 30Kg. ¿Cómo sería el polipasto que tendría que construir?
MECANISMOS DE TRANSFORMACIÓN
De Cambio de Velocidad
Estos mecanismos se usan para convertir una velocidad de entrada en otra diferente de salida.
Conceptos previos:
- Al ser mecanismo giratorios, la velocidad que usaremos es la Velocidad en r.p.m.= revoluciones por minuto.
Es decir las vueltas que se darán en un minuto.
Un eje que gira a una velocidad de 1500rpm quiere decir que dará 1500 vueltas en un minuto.
- La relación de velocidad es la cantidad de veces que el mecanismo va más rápido o lento a la salida que a la entrada.
Siempre se deja en forma de fracción.
La fórmula es
Rv= Vs/Ve
Donde Rv = relación de velocidad; Vs= velocidad de salida Ve= velocidad de entrada.
Veamos unos ejemplos:
- Rv=1/1 El mecanismo tiene la misma velocidad a la entrada que a la salida.
- Rv = 1/5 El mecanismo reduce la velocidad 5 veces a la Salida.
Si a la entrada tiene una velocidad de 5000rpm, a la Salida tendrá una velocidad de 1000rpm.
Será un Mecanismo Reductor de Velocidad.
- Rv= 5/1 El mecanismo va 5 veces más rápido a la salida que a la entrada.
Si a la entrada tiene una velocidad de 5000rpm a la salida tendrá una velocidad de 25000rpm.
Será un Mecanismo Multiplicador de Velocidad.
Recuerda ¡¡¡Siempre en forma de fracción!!!.
Ahora que tenemos esto claro, veamos el estudio de estos mecanismos.
- Ruedas de Fricción: El movimiento se transmite de una rueda a otra mediante fricción =rozamiento.

Fórmula: D1 x V1 = D2 x V2
D1= diámetro de la rueda 1
D2= diámetro de la rueda 2
V1=velocidad de la rueda 1 (en r.p.m.)
V2=velocidad de la rueda 2 (en r.p.m.)
Recuerda que la rueda motriz es la que está enganchada al motor.
Dependiendo si la rueda motriz es la grande o la pequeña será reductor o multiplicador de velocidad.
En algunos sitios podemos encontrarnos que a V1 se le llama N1 y a V2 = N2, pero es lo mismo.
Se pone N para expresar que es velocidad en rpm.
- Poleas de Transmisión o Sistema de Poleas: son dos o más poleas unidas que se transmite de unas a otras el movimiento circular por medio de una correa de transmisión.
Si son más de 2 poleas se llaman Tren de Poleas:

En el caso de arriba si la polea 1 gira a la derecha todas las demás también giran a la derecha.
¿Qué tendríamos que hacer si queremos cambiar el giro de la polea de salida?

Simplemente se debe cruzar la correa de transmisión.
Fórmula de los sistemas de poleas simples de 2 poleas:
Diámetro de la 1 x Velocidad de la 1 = Diámetro de la 2 x Velocidad de la 2;
Resumido: D1 x V1 = D2 x V2; recuerda V en r.p.m. y los dos diámetros en la misma unidad.
En esta ecuación siempre nos darán 3 datos y tendremos que calcular el cuarto.
Al final siempre calcularemos la relación de velocidad total del sistema.
Cuando tenemos más de 2 poleas tendremos que dividir el tren en los diferentes sistemas simples que tenga e ir calculando con la fórmula anterior uno a uno. Veamos un ejemplo:
Calcula la velocidad de salida y la relación de velocidades del siguiente tren de poleas sabiendo que se engancha un motor de 20.000rpm en la polea 1.

Como ves tenemos dos sistemas simples, el formado por las poleas 1-2 y el formado por las poleas 3-4. Empezamos por el primero.
Sistema 1-2)
D1 x V1 = D2 x V2 ==> 10cm x 20.000rpm = 50cm x V2 ==> Despejando V2 tenemos:
V2 = (10 x 20.000) / 50 = 4.000 rpm.
Ahora vamos por el segundo.
Sistema 3-4)
D3 x V3 = D4 x V4; ¿Qué datos tenemos? D3 y D4 solo pero fíjate que al estar las poleas 2 y 3 en el mismo eje las dos tiene que girar a la misma velocidad obligatoriamente, por lo que V2=V3= 4.000rpm.
Ahora ya tenemos 3 datos de la ecuación y solo nos queda despejar el cuarto, la V4.
10cm x 4.000rpm = 50cm x V4 ==> Despejando V4 tenemos:
V4 = (10 x 4000)/ 50 = 800 rpm. Problema resuelto.
¿Seguro?
NO, nos queda calcular la relación de velocidad.
Rv = Vs/Ve = 800/20.000 = 8/200 = 1/25 ==> Sistema Reductor de Velocidad.
Reduce 25 veces la velocidad de entrada a la salida.
Esta Rv siempre será la misma para este mecanismo, nunca cambiará y además no tiene unidad.
Imagina que en el mismo tren de poleas queremos cambiar el motor por otro que gira a 25.000 rpm.
¿A qué velocidad girará la velocidad de salida o 4?
Muy fácil, no tendremos que volver hacer todos los cálculos, ya que podemos utilizar la relación de velocidad:
Rv = Vs / Ve ==> tenemos todo menos la Vs, pues a despejarla ==>
Vs =Rv x Ve = (1/25) x 25.000 rpm = 1000rpm.
Y así para cualquier velocidad del motor. Esta es la importancia de calcular en cualquier mecanismo la Rv.
Si sabemos la Rv del mecanismo podemos calcular la velocidad de salida en función de la de entrada para cualquier velocidad e incluso sin conocer cuantas poleas tiene el mecanismo.
- Sistema de Poleas de Conos Invertidos o Caja de Velocidades: están formadas por varias poleas de diferente diámetro montadas sobre el mismo eje, al que permanecen unidas mediante un sistema de fijación fijo.
Estas poleas se unen a otro eje mediante la correa de transmisión pero el eje de salida tendrá las mismas poleas pero invertidas.
Veamos un ejemplo de aplicación en un taladro de columna:

El motor siempre girará a la misma velocidad, pero la broca girará a una u otra velocidad dependiendo donde coloquemos la correa de transmisión.
Solo hay que calcular el sistema de polea simple que una la correa de transmisión en la posición que este.
Uno de los problemas de los sistemas de poleas es que la correa de transmisión puede patinar y se pierde transmisión, o incluso podría romperse y el sistema dejaría de funcionar.
La solución a estos problemas la tenemos usando los engranajes.
- Engranajes: son mecanismos formados por varias ruedas dentadas unidas.
No necesitan correa de transmisión.

El de la derecha será un engranaje simple y el de la izquierda un tren de engranajes.
Para calcular estos mecanismos es muy parecido a los sistemas de poleas, cambiando el diámetro por el número de dientes de cada rueda.
Su fórmula es:
Número de dientes de la rueda 1 x Velocidad de la rueda 1 = Número dientes rueda 2 x Velocidad rueda 2.
Fórmula de Engranajes: Z1 x N1 = Z2 x N2 ==>
Donde Z es el número de dientes N la velocidad en rpm (revoluciones o vueltas por minuto).
La velocidad en rpm se llama N para no confundirla con la velocidad V en metros/segundo, que son diferentes.
De estos 4 datos de la fórmula conoceremos siempre 3 y lo que tenemos que hacer es despejar el dato que nos falte.
Vamos a calcular un engranaje sencillo.
Si la rueda 1 es la motriz y gira a 100rpm con 10 dientes.
¿A qué velocidad girará 2 con 20 dientes?
(OJO como están colocadas las ruedas dentadas, al revés de como hasta ahora, la motriz que lleva el movimiento es la de la izquierda).
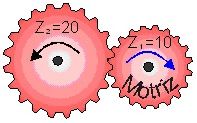
Z1 x N1 = Z2 x N2;
10 x 100rpm = 20 x N2;
N2 = (10 x 100) / 20 =50 rpm
La rueda conducida o de salida girará a 50rpm, luego es un engranaje reductor de velocidad. ¿Fácil No?.
Esto no es magia, todo lo que pierde por un lado lo ganará por otro y viceversa.
"Cuando un engranaje reduce su velocidad, todo lo que pierde en velocidad, lo gana en par motor (fuerza)"
Par Motor = momento de la fuerza que ejerce sobre el eje de rotación, o lo que es lo mismo la tendencia de una fuerza para girar un objeto alrededor de su eje.
Al reducir la velocidad el eje tendrá más par motor o fuerza para girar (mover) objetos.
Calculo de Tren de Engranajes
Ya sabemos que cuando tenemos más de dos ruedas dentadas en el engranaje se llama tren de engranajes.
Como las ruedas dentadas son complicadas de dibujar utilizamos símbolos para su representación.
¿Mucho más fácil NO?
Fíjate que las ruedas simples se representan con una línea vertical que será más o menos larga en función del número de dientes.
Las compuestas (dos ruedas sobre un mismo eje) se representan con dos líneas verticales separadas.
Imagina que la velocidad de entrada del tren de engranaje de la figura (podríamos conectar un motor al engranaje) fuera de 400 rpm.
Ahora fíjate que realmente tenemos dos engranes simples dentro del tren, la rueda 1 (la del motor) con la 2 y la rueda 3 con la 4.
La rueda 2 y la 3 van sobre el mismo eje y por lo tanto giran a la misma velocidad en rpm.
Se llama rueda dentada doble o compuesta.

Na = Nb = Velocidad del eje en revoluciones por minuto.
Para empezar los cálculos descomponemos el sistema en los dos engranajes simples.
Tenemos el 1-2 y el 3-4.
Calculamos cada uno de forma independiente.
Recuerda que la 2 y la 3 al estar en el mismo eje tendrán la misma velocidad en rpm.
Las vueltas que de el eje por minuto serán las vueltas que den las dos ruedas en un minuto.
Sistema 1-2) Z1 x N1 = Z2 x N2 ==> 10 x 400 = 50 x N2
Despejamos N2 = (10 x 400) /50 = 80 rpm Recuerda esta N2 será la misma que la N3.
Sistema 3-4) Z3 x N3 = Z4 x N4 ==> 10 x 80 = 50 x N4
Despejamos N4 = (10 x 80)/50 = 16 rpm ==> Sistema Reductor de velocidad.
Ya tenemos calculada la velocidad de salida del tren de engranaje.
Por su importancia hemos hecho una página especial hablando sobre este tipo de mecanismos.
Tienes mucho más sobre los engranajes en el siguiente enlace= Engranajes.
- Sistema de Engranajes con Cadena: son dos ruedas o más ruedas dentadas unidas por una cadena de eslabones.
Estos mecanismos se calculan exactamente igual que los engranajes anteriores.
La ventaja de estos mecanismos es que podemos tener las ruedas dentadas separadas gracias a la cadena.

- Tornillo sin fin-rueda dentada: Es un tornillo sin fin unido a una rueda dentada.
Es un mecanismo gran reductor de velocidad ya que por cada vuelta que da el tornillo la rueda gira un solo diente.
NO es reversible, el motor siempre tiene que ir en el tornillo sin fin.
Si lo ponemos en la rueda dentada el mecanismo se trabaría y no gira.

Fórmula: Vsalida = Vmotor/Número de dientes de la rueda
Vs = Vm x Z; recuerda que la velocidad del motor siempre es la velocidad del tornillo sin fin.
En el ejemplo del dibujo imagina que el motor gira a 1000rpm y la rueda tiene 50 dientes.
Vs = 1000/50 = 20rpm
¡¡¡Reducirá 50 veces la velocidad de salida en el eje de la rueda!!!. Rv = 1/50.
Nota: cuando un mecanismo reduce la velocidad no es magia, todo lo que pierde en velocidad lo gana en fuerza y si aumenta la velocidad, todo lo que gana en velocidad lo pierde en fuerza.
Estos mecanismos se usan mucho para los ascensores.
Si por una casualidad el motor se parase, el peso del ascensor intentaría hacer girar la rueda para caer, pero al no ser reversible el sistema se trabaría y el ascensor no se caería.
Ejercicios:
1. Calcula la velocidad de salida y la relación de velocidad final del engranaje de la figura:

2. ¿Cuál será la velocidad de salida y la Rv de un sistema de tornillo sin fin- rueda dentada si se coloca un motor de 1000rpm al tornillo sin fin y la rueda dentada tiene 10 dientes?
¿Y si se coloca el motor en la rueda dentada?
MECANISMOS QUE TRANSFORMAN EL MOVIMIENTO
- Tornillo-Tuerca: Se emplea en la conversión de un movimiento giratorio en lineal.
Al girar el tornillo la tuerca se desplaza en movimiento rectilíneo.
Es un mecanismo muy reductor, si la velocidad del tornillo es muy grande el desplazamiento de la tuerca es lento y lineal.
Si quieres saber más: Tuercas y Tornillos.

- Mecanismo de Piñón-Cremallera: es una rueda dentada enganchada a una cremallera.
El movimiento giratorio de la rueda se transforma en lineal en la cremallera o viceversa.

- Biela-Manivela: mecanismo de transmisión y transformación de movimiento giratorio en lineal o viceversa.

- Cigüeñal: es un eje acodado que al girar describe una circunferencia.
Normalmente no se usa solo, se suele acoplar una barra llamada biela.

- Biela-Cigüeñal: el movimiento giratorio del cigüeñal se transforma en rectilíneo de vaivén en la biela o viceversa.

En los motores de los coches solemos tener un cigüeñal con 4 o 6 codos y bielas.
A las bielas se les llama pistones.
Estos pistones van encerrados en los cilindros, en los que se mueven de arriba abajo por la explosión del combustible, haciendo girar el cigüeñal y este a su vez mueve las ruedas del coche.

- Leva: es un elemento mecánico que está sujeto a un eje por un punto que no es su centro geométrico y en la mayoría de los casos es de forma ovoide.
Al girar empuja una pieza llamada seguidor hacia arriba o abajo.

- Excéntrica: es igual que la leva pero su forma es circular.
Su centro de giro no esta en el centro del círculo de la excéntrica.
- Trinquete: básicamente está formado por una rueda dentada y una uñeta que puede estar accionada por su propio peso o por un mecanismo de resorte.
La uñeta hace de freno, impidiendo el giro de la rueda dentada en el sentido no permitido.
Permite el giro de un eje en un solo sentido.

OTROS MECANISMOS
MECANISMOS PARA REGULAR EL MOVIMIENTO
- Los frenos: en este enlace: Sistema de frenos.
MECANISMOS PARA ACOPLAMIENTO DE EJES
- Embragues de fricción: se unen dos superficies para acoplar los dos ejes.

- Embrague de dientes: el acoplamiento tiene lugar cuando encajan los dientes de uno y otro eje.

- Juntas Oldham y Cardan: las Oldham para unir ejes no alineados y las cardan para unir ejes en ángulo.

MECANISMOS PARA ACUMULAR ENERGÍA
- Los Muelles: los muelles absorben energía cuando se les somete a presión.
Esta energía pueden liberarla más tarde.

- Amortiguadores: los amortiguadores están formados por muelles helicoidales de acero.
La función más importante de los amortiguadores es mantener las ruedas siempre en contacto con la carretera.

- Los soportes son elementos que sirven de apoyo a los ejes o árboles.
Hay dos fundamentales: cojinetes y rodamientos.
- Los cojinetes no giran con el eje. El eje gira sobre su agujero.
- Los rodamientos giran en su interior con el Eje.

Es muy importante dentro de los mecanismos la lubricación de los mismos para evitar el desgaste y la rotura.
Aquí te dejamos un enlace que habla de todo esto: Lubricación.
Ahora sería bueno que fuera a los: Ejercicios Sobre Mecanismos
Si te ha gustado haz click en Compartir, Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
Pero primero empecemos por dejar claro que es eso de un mecanismo.
¿Qué son los Mecanismos?
Son elementos destinados a transmitir y/o transformar fuerzas y/o movimientos desde un elemento motriz (motor) a un elemento conducido (receptor), con la misión de permitir al ser humano realizar determinados trabajos con mayor comodidad y menor esfuerzo.

Existen 3 grupos principales de mecanismos:
1. Mecanismos de transmisión: se utilizan para modificar la fuerza de entrada por otra diferente de salida. Transmiten fuerzas de un sitio a otro.
2. Mecanismos de transformación: son aquellos en los que el elemento motriz y el conducido tienen distinto tipo de movimiento.
Transforman la velocidad de entrada en otra diferente de salida o transforman el movimiento de entrada en otro diferente de salida.
Por ejemplo un tornillo-tuerca, el tornillo gira y la tuerca se desplaza lineal o el sistema de poleas donde la velocidad de entrada se transforma en otra diferente de salida.
3. Otros Mecanismos: Aquí se agrupan todos los demás.
Tenemos mecanismos para regular el movimiento, por ejemplo los frenos, para acoplar o desacoplar ejes, por ejemplo los embragues y mecanismos que acumulan energía, por ejemplo los muelles.
Antes de empezar a estudiar los mecanismos tenemos que decir que la unidad correcta de la fuerza y el peso es el Newton.
Resulta que en la vida diaria nadie dice peso 40 Newtons, todo el mundo utiliza la unidad del Kilogramo, aunque estaría mal usada.
Como tecnología es un área sumamente práctica nosotros utilizaremos el Kg, aunque ya sabemos que físicamente es incorrecto.
Empecemos el estudio uno a uno.
MECANISMOS DE TRANSMISIÓN
LAS POLEAS
Se utilizan para subir o bajar cargas pesadas con menos esfuerzo.
- Polea Simple o Fija: es una rueda que tiene un ranura o acanaladura en su periferia, que gira alrededor de un eje que pasa por su centro.
Su fórmula es: Fuerza = Resistencia.
Resistencia es el peso que queremos subir con la polea y fuerza es el esfuerzo que tenemos que hacer para subir el peso.

Para levantar 20Kg necesitamos hacer una fuerza de 20Kg. La pregunta es…¿Cual es la ventaja?
Es más fácil levantar un peso tirando hacia arriba y además el peso de nuestro propio peso nos ayuda a levantar.
Si yo pesara 30Kg para levantar los 20Kg solo tendría que colgarme para subirlo.
- Polea móvil o compuesta: Es un conjunto de dos poleas, una de las cuales es fija, mientras que la otra es móvil.
La polea móvil dispone de un sistema armadura-gancho que le permite arrastrar la carga consigo al tirar de la cuerda.
Fórmula: Fuerza = Peso/2

En este tipo de poleas tenemos la ventaja de la polea fija y además la fuerza necesaria para levantar un peso es de la mitad.
- Polipasto: Este mecanismo está formado por grupos de poleas fijas y móviles.
Cuando tenemos más de una polea móvil le llamamos polipasto.
Por cada polea móvil siempre hay una fija; Número de poleas móviles = Numero de poleas fijas.
Su fórmula es: F = P/2n
Donde n es el número de poleas fijas o móviles que son siempre las mismas.

- Manivela Torno: Se trata de una barra acodada unida a un eje en el que se encuentra el torno que es un tambor alrededor del cual se enrolla una cuerda o cable para levantar un peso.
Su fórmula es: F x d = P x r
Donde d es la longitud de la barra y r el radio del tambor.
- Palanca o Balancin: es una barra rígida que oscila sobre un punto de apoyo debido a la acción de dos fuerzas contrapuestas, la fuerza o potencia y la resistencia.

Antes de seguir con los siguientes mecanismos te dejamos unos ejercicios para practicar los vistos hasta aquí.
1º) Escribe la fórmula de equilibrio de un balancín.
2º) Calcula la fuerza que se puede levantar con un balancín haciendo una fuerza de 40Kg sobre una barra de 10m, si la barra donde ponemos el peso es de 2m.
3º)a) Cuál es la fórmula de la polea simple?
b) Cuál es la ventaja de una polea simple?
4º) Calcula la fuerza necesaria para levantar un peso de 70Kg con una polea móvil.
5º) ¿Qué fuerza necesitamos para levantar 2000Kg con un polipasto de 3 poleas móviles?
6º) Para levantar un peso de 2000Kg con un mecanismo de manivela-torno que tiene una barra de 50cm, en un tambor de 30cm de radio. ¿Qué fuerza necesitaríamos hacer?
7º) Quiero levantar un peso de 600Kg haciendo una fuerza de 30Kg. ¿Cómo sería el polipasto que tendría que construir?
MECANISMOS DE TRANSFORMACIÓN
De Cambio de Velocidad
Estos mecanismos se usan para convertir una velocidad de entrada en otra diferente de salida.
Conceptos previos:
- Al ser mecanismo giratorios, la velocidad que usaremos es la Velocidad en r.p.m.= revoluciones por minuto.
Es decir las vueltas que se darán en un minuto.
Un eje que gira a una velocidad de 1500rpm quiere decir que dará 1500 vueltas en un minuto.
- La relación de velocidad es la cantidad de veces que el mecanismo va más rápido o lento a la salida que a la entrada.
Siempre se deja en forma de fracción.
La fórmula es
Rv= Vs/Ve
Donde Rv = relación de velocidad; Vs= velocidad de salida Ve= velocidad de entrada.
Veamos unos ejemplos:
- Rv=1/1 El mecanismo tiene la misma velocidad a la entrada que a la salida.
- Rv = 1/5 El mecanismo reduce la velocidad 5 veces a la Salida.
Si a la entrada tiene una velocidad de 5000rpm, a la Salida tendrá una velocidad de 1000rpm.
Será un Mecanismo Reductor de Velocidad.
- Rv= 5/1 El mecanismo va 5 veces más rápido a la salida que a la entrada.
Si a la entrada tiene una velocidad de 5000rpm a la salida tendrá una velocidad de 25000rpm.
Será un Mecanismo Multiplicador de Velocidad.
Recuerda ¡¡¡Siempre en forma de fracción!!!.
Ahora que tenemos esto claro, veamos el estudio de estos mecanismos.
- Ruedas de Fricción: El movimiento se transmite de una rueda a otra mediante fricción =rozamiento.
Fórmula: D1 x V1 = D2 x V2
D1= diámetro de la rueda 1
D2= diámetro de la rueda 2
V1=velocidad de la rueda 1 (en r.p.m.)
V2=velocidad de la rueda 2 (en r.p.m.)
Recuerda que la rueda motriz es la que está enganchada al motor.
Dependiendo si la rueda motriz es la grande o la pequeña será reductor o multiplicador de velocidad.
En algunos sitios podemos encontrarnos que a V1 se le llama N1 y a V2 = N2, pero es lo mismo.
Se pone N para expresar que es velocidad en rpm.
- Poleas de Transmisión o Sistema de Poleas: son dos o más poleas unidas que se transmite de unas a otras el movimiento circular por medio de una correa de transmisión.
Si son más de 2 poleas se llaman Tren de Poleas:

En el caso de arriba si la polea 1 gira a la derecha todas las demás también giran a la derecha.
¿Qué tendríamos que hacer si queremos cambiar el giro de la polea de salida?

Simplemente se debe cruzar la correa de transmisión.
Fórmula de los sistemas de poleas simples de 2 poleas:
Diámetro de la 1 x Velocidad de la 1 = Diámetro de la 2 x Velocidad de la 2;
Resumido: D1 x V1 = D2 x V2; recuerda V en r.p.m. y los dos diámetros en la misma unidad.
En esta ecuación siempre nos darán 3 datos y tendremos que calcular el cuarto.
Al final siempre calcularemos la relación de velocidad total del sistema.
Cuando tenemos más de 2 poleas tendremos que dividir el tren en los diferentes sistemas simples que tenga e ir calculando con la fórmula anterior uno a uno. Veamos un ejemplo:
Calcula la velocidad de salida y la relación de velocidades del siguiente tren de poleas sabiendo que se engancha un motor de 20.000rpm en la polea 1.

Como ves tenemos dos sistemas simples, el formado por las poleas 1-2 y el formado por las poleas 3-4. Empezamos por el primero.
Sistema 1-2)
D1 x V1 = D2 x V2 ==> 10cm x 20.000rpm = 50cm x V2 ==> Despejando V2 tenemos:
V2 = (10 x 20.000) / 50 = 4.000 rpm.
Ahora vamos por el segundo.
Sistema 3-4)
D3 x V3 = D4 x V4; ¿Qué datos tenemos? D3 y D4 solo pero fíjate que al estar las poleas 2 y 3 en el mismo eje las dos tiene que girar a la misma velocidad obligatoriamente, por lo que V2=V3= 4.000rpm.
Ahora ya tenemos 3 datos de la ecuación y solo nos queda despejar el cuarto, la V4.
10cm x 4.000rpm = 50cm x V4 ==> Despejando V4 tenemos:
V4 = (10 x 4000)/ 50 = 800 rpm. Problema resuelto.
¿Seguro?
NO, nos queda calcular la relación de velocidad.
Rv = Vs/Ve = 800/20.000 = 8/200 = 1/25 ==> Sistema Reductor de Velocidad.
Reduce 25 veces la velocidad de entrada a la salida.
Esta Rv siempre será la misma para este mecanismo, nunca cambiará y además no tiene unidad.
Imagina que en el mismo tren de poleas queremos cambiar el motor por otro que gira a 25.000 rpm.
¿A qué velocidad girará la velocidad de salida o 4?
Muy fácil, no tendremos que volver hacer todos los cálculos, ya que podemos utilizar la relación de velocidad:
Rv = Vs / Ve ==> tenemos todo menos la Vs, pues a despejarla ==>
Vs =Rv x Ve = (1/25) x 25.000 rpm = 1000rpm.
Y así para cualquier velocidad del motor. Esta es la importancia de calcular en cualquier mecanismo la Rv.
Si sabemos la Rv del mecanismo podemos calcular la velocidad de salida en función de la de entrada para cualquier velocidad e incluso sin conocer cuantas poleas tiene el mecanismo.
- Sistema de Poleas de Conos Invertidos o Caja de Velocidades: están formadas por varias poleas de diferente diámetro montadas sobre el mismo eje, al que permanecen unidas mediante un sistema de fijación fijo.
Estas poleas se unen a otro eje mediante la correa de transmisión pero el eje de salida tendrá las mismas poleas pero invertidas.
Veamos un ejemplo de aplicación en un taladro de columna:

El motor siempre girará a la misma velocidad, pero la broca girará a una u otra velocidad dependiendo donde coloquemos la correa de transmisión.
Solo hay que calcular el sistema de polea simple que una la correa de transmisión en la posición que este.
Uno de los problemas de los sistemas de poleas es que la correa de transmisión puede patinar y se pierde transmisión, o incluso podría romperse y el sistema dejaría de funcionar.
La solución a estos problemas la tenemos usando los engranajes.
- Engranajes: son mecanismos formados por varias ruedas dentadas unidas.
No necesitan correa de transmisión.

El de la derecha será un engranaje simple y el de la izquierda un tren de engranajes.
Para calcular estos mecanismos es muy parecido a los sistemas de poleas, cambiando el diámetro por el número de dientes de cada rueda.
Su fórmula es:
Número de dientes de la rueda 1 x Velocidad de la rueda 1 = Número dientes rueda 2 x Velocidad rueda 2.
Fórmula de Engranajes: Z1 x N1 = Z2 x N2 ==>
Donde Z es el número de dientes N la velocidad en rpm (revoluciones o vueltas por minuto).
La velocidad en rpm se llama N para no confundirla con la velocidad V en metros/segundo, que son diferentes.
De estos 4 datos de la fórmula conoceremos siempre 3 y lo que tenemos que hacer es despejar el dato que nos falte.
Vamos a calcular un engranaje sencillo.
Si la rueda 1 es la motriz y gira a 100rpm con 10 dientes.
¿A qué velocidad girará 2 con 20 dientes?
(OJO como están colocadas las ruedas dentadas, al revés de como hasta ahora, la motriz que lleva el movimiento es la de la izquierda).

Z1 x N1 = Z2 x N2;
10 x 100rpm = 20 x N2;
N2 = (10 x 100) / 20 =50 rpm
La rueda conducida o de salida girará a 50rpm, luego es un engranaje reductor de velocidad. ¿Fácil No?.
Esto no es magia, todo lo que pierde por un lado lo ganará por otro y viceversa.
"Cuando un engranaje reduce su velocidad, todo lo que pierde en velocidad, lo gana en par motor (fuerza)"
Par Motor = momento de la fuerza que ejerce sobre el eje de rotación, o lo que es lo mismo la tendencia de una fuerza para girar un objeto alrededor de su eje.
Al reducir la velocidad el eje tendrá más par motor o fuerza para girar (mover) objetos.
Calculo de Tren de Engranajes
Ya sabemos que cuando tenemos más de dos ruedas dentadas en el engranaje se llama tren de engranajes.
Como las ruedas dentadas son complicadas de dibujar utilizamos símbolos para su representación.
¿Mucho más fácil NO?
Fíjate que las ruedas simples se representan con una línea vertical que será más o menos larga en función del número de dientes.
Las compuestas (dos ruedas sobre un mismo eje) se representan con dos líneas verticales separadas.
Imagina que la velocidad de entrada del tren de engranaje de la figura (podríamos conectar un motor al engranaje) fuera de 400 rpm.
Ahora fíjate que realmente tenemos dos engranes simples dentro del tren, la rueda 1 (la del motor) con la 2 y la rueda 3 con la 4.
La rueda 2 y la 3 van sobre el mismo eje y por lo tanto giran a la misma velocidad en rpm.
Se llama rueda dentada doble o compuesta.

Na = Nb = Velocidad del eje en revoluciones por minuto.
Para empezar los cálculos descomponemos el sistema en los dos engranajes simples.
Tenemos el 1-2 y el 3-4.
Calculamos cada uno de forma independiente.
Recuerda que la 2 y la 3 al estar en el mismo eje tendrán la misma velocidad en rpm.
Las vueltas que de el eje por minuto serán las vueltas que den las dos ruedas en un minuto.
Sistema 1-2) Z1 x N1 = Z2 x N2 ==> 10 x 400 = 50 x N2
Despejamos N2 = (10 x 400) /50 = 80 rpm Recuerda esta N2 será la misma que la N3.
Sistema 3-4) Z3 x N3 = Z4 x N4 ==> 10 x 80 = 50 x N4
Despejamos N4 = (10 x 80)/50 = 16 rpm ==> Sistema Reductor de velocidad.
Ya tenemos calculada la velocidad de salida del tren de engranaje.
Por su importancia hemos hecho una página especial hablando sobre este tipo de mecanismos.
Tienes mucho más sobre los engranajes en el siguiente enlace= Engranajes.
- Sistema de Engranajes con Cadena: son dos ruedas o más ruedas dentadas unidas por una cadena de eslabones.
Estos mecanismos se calculan exactamente igual que los engranajes anteriores.
La ventaja de estos mecanismos es que podemos tener las ruedas dentadas separadas gracias a la cadena.
- Tornillo sin fin-rueda dentada: Es un tornillo sin fin unido a una rueda dentada.
Es un mecanismo gran reductor de velocidad ya que por cada vuelta que da el tornillo la rueda gira un solo diente.
NO es reversible, el motor siempre tiene que ir en el tornillo sin fin.
Si lo ponemos en la rueda dentada el mecanismo se trabaría y no gira.
Fórmula: Vsalida = Vmotor/Número de dientes de la rueda
Vs = Vm x Z; recuerda que la velocidad del motor siempre es la velocidad del tornillo sin fin.
En el ejemplo del dibujo imagina que el motor gira a 1000rpm y la rueda tiene 50 dientes.
Vs = 1000/50 = 20rpm
¡¡¡Reducirá 50 veces la velocidad de salida en el eje de la rueda!!!. Rv = 1/50.
Nota: cuando un mecanismo reduce la velocidad no es magia, todo lo que pierde en velocidad lo gana en fuerza y si aumenta la velocidad, todo lo que gana en velocidad lo pierde en fuerza.
Estos mecanismos se usan mucho para los ascensores.
Si por una casualidad el motor se parase, el peso del ascensor intentaría hacer girar la rueda para caer, pero al no ser reversible el sistema se trabaría y el ascensor no se caería.
Ejercicios:
1. Calcula la velocidad de salida y la relación de velocidad final del engranaje de la figura:

2. ¿Cuál será la velocidad de salida y la Rv de un sistema de tornillo sin fin- rueda dentada si se coloca un motor de 1000rpm al tornillo sin fin y la rueda dentada tiene 10 dientes?
¿Y si se coloca el motor en la rueda dentada?
MECANISMOS QUE TRANSFORMAN EL MOVIMIENTO
- Tornillo-Tuerca: Se emplea en la conversión de un movimiento giratorio en lineal.
Al girar el tornillo la tuerca se desplaza en movimiento rectilíneo.
Es un mecanismo muy reductor, si la velocidad del tornillo es muy grande el desplazamiento de la tuerca es lento y lineal.
Si quieres saber más: Tuercas y Tornillos.

- Mecanismo de Piñón-Cremallera: es una rueda dentada enganchada a una cremallera.
El movimiento giratorio de la rueda se transforma en lineal en la cremallera o viceversa.

- Biela-Manivela: mecanismo de transmisión y transformación de movimiento giratorio en lineal o viceversa.

- Cigüeñal: es un eje acodado que al girar describe una circunferencia.
Normalmente no se usa solo, se suele acoplar una barra llamada biela.

- Biela-Cigüeñal: el movimiento giratorio del cigüeñal se transforma en rectilíneo de vaivén en la biela o viceversa.

En los motores de los coches solemos tener un cigüeñal con 4 o 6 codos y bielas.
A las bielas se les llama pistones.
Estos pistones van encerrados en los cilindros, en los que se mueven de arriba abajo por la explosión del combustible, haciendo girar el cigüeñal y este a su vez mueve las ruedas del coche.

- Leva: es un elemento mecánico que está sujeto a un eje por un punto que no es su centro geométrico y en la mayoría de los casos es de forma ovoide.
Al girar empuja una pieza llamada seguidor hacia arriba o abajo.
- Excéntrica: es igual que la leva pero su forma es circular.
Su centro de giro no esta en el centro del círculo de la excéntrica.
- Trinquete: básicamente está formado por una rueda dentada y una uñeta que puede estar accionada por su propio peso o por un mecanismo de resorte.
La uñeta hace de freno, impidiendo el giro de la rueda dentada en el sentido no permitido.
Permite el giro de un eje en un solo sentido.
OTROS MECANISMOS
MECANISMOS PARA REGULAR EL MOVIMIENTO
- Los frenos: en este enlace: Sistema de frenos.
MECANISMOS PARA ACOPLAMIENTO DE EJES
- Embragues de fricción: se unen dos superficies para acoplar los dos ejes.

- Embrague de dientes: el acoplamiento tiene lugar cuando encajan los dientes de uno y otro eje.

- Juntas Oldham y Cardan: las Oldham para unir ejes no alineados y las cardan para unir ejes en ángulo.

MECANISMOS PARA ACUMULAR ENERGÍA
- Los Muelles: los muelles absorben energía cuando se les somete a presión.
Esta energía pueden liberarla más tarde.

- Amortiguadores: los amortiguadores están formados por muelles helicoidales de acero.
La función más importante de los amortiguadores es mantener las ruedas siempre en contacto con la carretera.

- Los soportes son elementos que sirven de apoyo a los ejes o árboles.
Hay dos fundamentales: cojinetes y rodamientos.
- Los cojinetes no giran con el eje. El eje gira sobre su agujero.
- Los rodamientos giran en su interior con el Eje.

Es muy importante dentro de los mecanismos la lubricación de los mismos para evitar el desgaste y la rotura.
Aquí te dejamos un enlace que habla de todo esto: Lubricación.
Ahora sería bueno que fuera a los: Ejercicios Sobre Mecanismos
Si te ha gustado haz click en Compartir, Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
TAMBIEN TE PUEDE INTERESAR
Todo Sobre Mecanismos
Ejercicios Mecanismos
Mecanismos
Revolucion Industrial y Maquina de Vapor
Motor de Combustion
Proyectos de Mecanismos
Sistema de Frenos
Freno Magnético
