CALCULO DE VIGAS
¿Qué es una Viga?
Una viga es un elemento de una estructura diseñada para soportar fuerzas.
Para soportar estas fuerzas la viga debe estar en equilibrio, es decir que no se rompa por las fuerzas y que no se mueva o gire (momentos).

Condiciones Necesarias Para el Equilibrio en Una Viga
- La suma de las fuerzas en el eje X = 0
- La suma de las fuerzas en el eje Y = 0
- Además la suma de los momentos de todas las fuerza debe ser 0.
Todas estas sumas son sumas vectoriales, ya que las fuerzas se representan por vectores y los momentos también.
Si quieres repasar los vectores te recomendamos el siguiente enlace: vectores.
Expliquemos primero que es eso del momento.
Momento de una fuerza respecto a un punto es el valor de la fuerza por la distancia al punto (distancia perpendicular a la fuerza).
Para calcularlo es muy fácil. Imaginemos una fuerza aplicada y un punto A. Queremos averiguar el momento de esa fuerza respecto a ese punto.

El momenta en A de la fuerza será Ma = F x da; donde da es la distancia perpendicular a la fuerza desde el punto A.
El momento de una fuerza lo que produce es un giro.
Para el cálculo de vigas tenemos entonces que averiguar las fuerzas y los momentos de las fuerzas aplicadas en las vigas.
Veamos un caso práctico:
Tenemos la viga con una fuerza exterior aplicada en el punto 2 y con dos apoyos simples en los extremos.
La viga se sujeta porque aparecen dos fuerzas en los puntos de apoyo en dirección contraria, como reacción a la fuerza externa del punto 2.
Tomamos como convenio de signos, fuerzas ascendentes positivas, fuerzas descendentes negativas.

Ya tenemos entonces que en esta viga hay 3 fuerzas, una hacia abajo y dos hacia arriba.
La suma de las fuerzas serán F1 + F3 - F2 = 0;
Para los momentos suponemos un punto sobre el que gira la viga y será sobre ese punto donde calcularemos los momentos.
En el ejemplo tomaremos como giro el punto 3, serán:
M1 = F1 x L;
L es la distancia desde el punto 1 al punto B.
M2 = F2 x L/2;
L/2 es la distancia desde el punto 2 al punto B.
M3 será cero por que la distancia es cero.

Ahora tenemos que hacer la suma de los momento, para eso debemos tener en cuenta que el signo de un momento en un punto (giro) de una fuerza hacia abajo es de signo contrario al momento (giro) que produce una fuerza hacia arriba en ese mismo punto.
La convención de signos que hemos elegido es que los momentos que producen un giro de la viga sobre el punto en sentido de las agujas del reloj son positivos y momentos que hacen girar la viga en sentido contrario al de las agujas del reloj son negativos.
Esta es la convención de signo más común, pero depende de ti, puedes hacerlo al revés.
Debes usar siempre la misma convención de signos a través de todo el problema.
Utiliza siempre el mismo convenio de signos desde el principio y no habrá problema.
M2 - M1 = 0. Que es lo que es lo mismo sustiyendo datos que ==> (F2 x L/2) - (F1 x L) = 0.
Con la ecuación de las fuerzas y la de los momentos ya podríamos calcular todo.
Normalmente se empieza por la de momentos para calcular la reacción (fuerza) en un apoyo, por ejemplo F1 y luego con la de fuerzas sacamos F3.
Si entendemos esto ya tenemos mucho camino avanzado, pero no es tan sencillo, las fuerzas y los momentos dependen del tipo de apoyo que tenga la viga.
Veamos los 3 más usados e importantes.

Veamos un ejercicios con una apoyo fijo a la izquierda (reacciones vertical y horizontal) y un apoyo en dilatación a la derecha (solo reacción vertical):

Tenemos una fuerza externa de 500 KN (kilonewtons) podrían ser Kg.
Como ves a partir de ahora a las fuerzas de las reacciones las llamaremos V o H si son verticales u horizontales.
Para resolver el ejercicio deberemos hacer las sumas de las fuerzas en la viga horizontales igual a cero y lo mismo para las verticales:
H1 = 0; solo hay una y su valor es cero.
V1 + V2 - 500KN = 0. No podemos calcular nada, por eso iremos a la ecuación de los momentos en el punto de la izquierda, punto 1:
(500 x 1) - (V2 x 4) = 0. Aqui podemos despejar el valor de V2.
V2 = (500 x 1)/4 = 125 KN. Ahora volvemos a la ecuación de fuerzas de arriba y podemos despejar V1.
V1 = 500 - 125 = 375KN. Problema resuelto.
Lo siguiente que nos suelen mandar en este tipo de ejercicios es hallar el diagrama de las fuerzas cortantes y de los momentos flectores.
Comencemos por el diagrama de esfuerzos cortantes.
Trazamos lineas de referencia desde la viga hacia abajo y en los puntos donde tengamos fuerzas o cargas externas y también el los puntos de apoyo (tendremos las reacciones).
También heremos una linea de referencia horizontal.
Ahora solo hay que representar el valor de las fuerzas en cada punto. En R1, estará V1 con valor de 375KN positivo.
Pues nada trazamos un punto con ese valor hacia arriba por ser positiva.
Ahora trazamos uná línea horizontal desde este valor hasta llegar a la siguiente fuerza, en este caso la de 500KN. En ese punto y a partir de él trazamos el valor de -500KN ya que es negativa.
Hacemos lo mismo hasta llegar a la reacción R2 y como V2 es positiva subimos su valor, es decir 125KN.
Ya tenemos nuestro diagrama de esfuerzo cortante.
Recuerda cuando no hay cargas se traza una línea horizontal desde el último punto. Aqui lo puedes ver:

Como ves lo último es sombrear las figuras geométricas que nos quedan formadas por las líneas (color amarillo).
Ahora nos toca hacer el diagrama de momentos flectores.
Como los momentos los hacemos desde el punto R1 el momento en ese punto para representarlo en el diagrama valdrá cero.
Ya tenemos nuestro primer punto de la curva de momentos.
Ahora vamos a calcular el diagrama por el método de las áreas, que es el más simple.
Para eso tenemos que tener en cuenta lo siguiente:
- Se suele dibujar debajo del diagrama de cortantes.
- Debajo de una línea horizontal del cortante se dibujo una linea inclinada en el de momentos y Debajo de una línea inclinada en el de cortantes, en el de momentos se dibujará una curva.
En nuestro ejercicio no habrá ninguna curva en el diagram de momentos por que no tenemos ninguna línea inclinada.
- Para sacar los valores se deben de calcular las áreas de las figuras geométricas del diagrama de cortantes.
Areas por encima de la linea de referencia de valor 0 serán positivas y las de por debajo de la linea de referencia serán negativos. Fíjate en nuestro ejemplo:
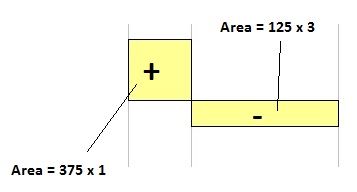
En nustro caso partimos de cero en R1 y tendremos una línea inclinada que llegará hasta el valor del área en el punto de la fuerza de 500KN.
Area positiva = 375 x 1m = 375m2
Area Negativa = 125 x 3 = 375 m2
Partimos el diagrama de cero en R1 (R1 es el punto desde donde determinamos los momentos y al ser la distancia cero el momento en ese punto será cero).
En la fuerza de 500KN el valor del áre será de 375. Marcamos ese punto.
El siguiente punto el siguiente será en la reacción R2 con valor de 375 pero hacia abajo por ser el área negativa.
Ahora siguiendo el criterio de lineas rectas en cortantes, se convierten en inclinadas en momentos, unimos los 3 puntos.
Aqui tienes los dos diagramas, en azul el de momentos, aunque se suele dibujar primero el de cortantes para poder sacar con el posteriormente el de momentos flectores.

Otro caso interesante envigas es cuando tenemos una fuerza externa repartida uniformemente por toda la viga o parte de ella o también llamada carga continua.
En estos casos todas las cargar repartidas uniformemente por la viga se convierten en una sola en el centro, cuyo valor será el valor de la fuerza por la distancia de un extremo a otro de la viga.
Mira como quedaría:

Ahora es el mismo caso que el anterior, así que deberíamos saber hacerlo.
Veamos un nuevo ejercicio un poco más complicado explicado en video:
Otro caso es el de la vigas empotradas. Veamos un caso de empotramiento con carga repartida.

La suma de los momentos en A debe ser igual a cero, y las fuerzas y reacciones en X y en Y también deben ser igual a cero.
Pero OJO si te fijas en los tipos de apoyos que vimos anteriormente, en un empotramiento tenemos en el punto de empotramiento un Momento Interno, que llamaremos en Ma y que ya no será cero y será de signo contrario al que ejercen las fuerzas externas, una reacción horizontal y otra vertical.
El momento del empotramiento es un momento de reacción para que la viga no gire, similar a las reacciones de las fuerzas.
Como la reacción horizontal será la única fuerza horizontal (en este caso) tendrá un calor de cero.
Esto es lo único que temos que tener en cuenta, a partir de ahora se hace como hemos explicado.
Mira este ejemplo con 4 fuerzas expresadas en To = toneladas.

Otro ejercicio de calculo de vigas resuelto:

Para hallar los diagramas de momentos hemos utilizado el llamado método de las áreas.
Ahora veamos otro método llamado método del corte en un punto de la viga, metodo de secciones o método de corte (los 3 son el mismo).
Este video nos lo explica muy bien:
Si te ha gustado haz click en Compartir, Gracias:
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
Una viga es un elemento de una estructura diseñada para soportar fuerzas.
Para soportar estas fuerzas la viga debe estar en equilibrio, es decir que no se rompa por las fuerzas y que no se mueva o gire (momentos).

Condiciones Necesarias Para el Equilibrio en Una Viga
- La suma de las fuerzas en el eje X = 0
- La suma de las fuerzas en el eje Y = 0
- Además la suma de los momentos de todas las fuerza debe ser 0.
Todas estas sumas son sumas vectoriales, ya que las fuerzas se representan por vectores y los momentos también.
Si quieres repasar los vectores te recomendamos el siguiente enlace: vectores.
Expliquemos primero que es eso del momento.
Momento de una fuerza respecto a un punto es el valor de la fuerza por la distancia al punto (distancia perpendicular a la fuerza).
Para calcularlo es muy fácil. Imaginemos una fuerza aplicada y un punto A. Queremos averiguar el momento de esa fuerza respecto a ese punto.

El momenta en A de la fuerza será Ma = F x da; donde da es la distancia perpendicular a la fuerza desde el punto A.
El momento de una fuerza lo que produce es un giro.
Para el cálculo de vigas tenemos entonces que averiguar las fuerzas y los momentos de las fuerzas aplicadas en las vigas.
Veamos un caso práctico:
Tenemos la viga con una fuerza exterior aplicada en el punto 2 y con dos apoyos simples en los extremos.
La viga se sujeta porque aparecen dos fuerzas en los puntos de apoyo en dirección contraria, como reacción a la fuerza externa del punto 2.
Tomamos como convenio de signos, fuerzas ascendentes positivas, fuerzas descendentes negativas.

Ya tenemos entonces que en esta viga hay 3 fuerzas, una hacia abajo y dos hacia arriba.
La suma de las fuerzas serán F1 + F3 - F2 = 0;
Para los momentos suponemos un punto sobre el que gira la viga y será sobre ese punto donde calcularemos los momentos.
En el ejemplo tomaremos como giro el punto 3, serán:
M1 = F1 x L;
L es la distancia desde el punto 1 al punto B.
M2 = F2 x L/2;
L/2 es la distancia desde el punto 2 al punto B.
M3 será cero por que la distancia es cero.

Ahora tenemos que hacer la suma de los momento, para eso debemos tener en cuenta que el signo de un momento en un punto (giro) de una fuerza hacia abajo es de signo contrario al momento (giro) que produce una fuerza hacia arriba en ese mismo punto.
La convención de signos que hemos elegido es que los momentos que producen un giro de la viga sobre el punto en sentido de las agujas del reloj son positivos y momentos que hacen girar la viga en sentido contrario al de las agujas del reloj son negativos.
Esta es la convención de signo más común, pero depende de ti, puedes hacerlo al revés.
Debes usar siempre la misma convención de signos a través de todo el problema.
Utiliza siempre el mismo convenio de signos desde el principio y no habrá problema.
M2 - M1 = 0. Que es lo que es lo mismo sustiyendo datos que ==> (F2 x L/2) - (F1 x L) = 0.
Con la ecuación de las fuerzas y la de los momentos ya podríamos calcular todo.
Normalmente se empieza por la de momentos para calcular la reacción (fuerza) en un apoyo, por ejemplo F1 y luego con la de fuerzas sacamos F3.
Si entendemos esto ya tenemos mucho camino avanzado, pero no es tan sencillo, las fuerzas y los momentos dependen del tipo de apoyo que tenga la viga.
Veamos los 3 más usados e importantes.
Tipos de Apoyos en las Vigas

Veamos un ejercicios con una apoyo fijo a la izquierda (reacciones vertical y horizontal) y un apoyo en dilatación a la derecha (solo reacción vertical):

Tenemos una fuerza externa de 500 KN (kilonewtons) podrían ser Kg.
Como ves a partir de ahora a las fuerzas de las reacciones las llamaremos V o H si son verticales u horizontales.
Para resolver el ejercicio deberemos hacer las sumas de las fuerzas en la viga horizontales igual a cero y lo mismo para las verticales:
H1 = 0; solo hay una y su valor es cero.
V1 + V2 - 500KN = 0. No podemos calcular nada, por eso iremos a la ecuación de los momentos en el punto de la izquierda, punto 1:
(500 x 1) - (V2 x 4) = 0. Aqui podemos despejar el valor de V2.
V2 = (500 x 1)/4 = 125 KN. Ahora volvemos a la ecuación de fuerzas de arriba y podemos despejar V1.
V1 = 500 - 125 = 375KN. Problema resuelto.
Lo siguiente que nos suelen mandar en este tipo de ejercicios es hallar el diagrama de las fuerzas cortantes y de los momentos flectores.
Comencemos por el diagrama de esfuerzos cortantes.
Trazamos lineas de referencia desde la viga hacia abajo y en los puntos donde tengamos fuerzas o cargas externas y también el los puntos de apoyo (tendremos las reacciones).
También heremos una linea de referencia horizontal.
Ahora solo hay que representar el valor de las fuerzas en cada punto. En R1, estará V1 con valor de 375KN positivo.
Pues nada trazamos un punto con ese valor hacia arriba por ser positiva.
Ahora trazamos uná línea horizontal desde este valor hasta llegar a la siguiente fuerza, en este caso la de 500KN. En ese punto y a partir de él trazamos el valor de -500KN ya que es negativa.
Hacemos lo mismo hasta llegar a la reacción R2 y como V2 es positiva subimos su valor, es decir 125KN.
Ya tenemos nuestro diagrama de esfuerzo cortante.
Recuerda cuando no hay cargas se traza una línea horizontal desde el último punto. Aqui lo puedes ver:

Como ves lo último es sombrear las figuras geométricas que nos quedan formadas por las líneas (color amarillo).
Ahora nos toca hacer el diagrama de momentos flectores.
Como los momentos los hacemos desde el punto R1 el momento en ese punto para representarlo en el diagrama valdrá cero.
Ya tenemos nuestro primer punto de la curva de momentos.
Ahora vamos a calcular el diagrama por el método de las áreas, que es el más simple.
Para eso tenemos que tener en cuenta lo siguiente:
- Se suele dibujar debajo del diagrama de cortantes.
- Debajo de una línea horizontal del cortante se dibujo una linea inclinada en el de momentos y Debajo de una línea inclinada en el de cortantes, en el de momentos se dibujará una curva.
En nuestro ejercicio no habrá ninguna curva en el diagram de momentos por que no tenemos ninguna línea inclinada.
- Para sacar los valores se deben de calcular las áreas de las figuras geométricas del diagrama de cortantes.
Areas por encima de la linea de referencia de valor 0 serán positivas y las de por debajo de la linea de referencia serán negativos. Fíjate en nuestro ejemplo:

En nustro caso partimos de cero en R1 y tendremos una línea inclinada que llegará hasta el valor del área en el punto de la fuerza de 500KN.
Area positiva = 375 x 1m = 375m2
Area Negativa = 125 x 3 = 375 m2
Partimos el diagrama de cero en R1 (R1 es el punto desde donde determinamos los momentos y al ser la distancia cero el momento en ese punto será cero).
En la fuerza de 500KN el valor del áre será de 375. Marcamos ese punto.
El siguiente punto el siguiente será en la reacción R2 con valor de 375 pero hacia abajo por ser el área negativa.
Ahora siguiendo el criterio de lineas rectas en cortantes, se convierten en inclinadas en momentos, unimos los 3 puntos.
Aqui tienes los dos diagramas, en azul el de momentos, aunque se suele dibujar primero el de cortantes para poder sacar con el posteriormente el de momentos flectores.

Otro caso interesante envigas es cuando tenemos una fuerza externa repartida uniformemente por toda la viga o parte de ella o también llamada carga continua.
En estos casos todas las cargar repartidas uniformemente por la viga se convierten en una sola en el centro, cuyo valor será el valor de la fuerza por la distancia de un extremo a otro de la viga.
Mira como quedaría:

Ahora es el mismo caso que el anterior, así que deberíamos saber hacerlo.
Veamos un nuevo ejercicio un poco más complicado explicado en video:
Otro caso es el de la vigas empotradas. Veamos un caso de empotramiento con carga repartida.

La suma de los momentos en A debe ser igual a cero, y las fuerzas y reacciones en X y en Y también deben ser igual a cero.
Pero OJO si te fijas en los tipos de apoyos que vimos anteriormente, en un empotramiento tenemos en el punto de empotramiento un Momento Interno, que llamaremos en Ma y que ya no será cero y será de signo contrario al que ejercen las fuerzas externas, una reacción horizontal y otra vertical.
El momento del empotramiento es un momento de reacción para que la viga no gire, similar a las reacciones de las fuerzas.
Como la reacción horizontal será la única fuerza horizontal (en este caso) tendrá un calor de cero.
Esto es lo único que temos que tener en cuenta, a partir de ahora se hace como hemos explicado.
Mira este ejemplo con 4 fuerzas expresadas en To = toneladas.

Otro ejercicio de calculo de vigas resuelto:

Para hallar los diagramas de momentos hemos utilizado el llamado método de las áreas.
Ahora veamos otro método llamado método del corte en un punto de la viga, metodo de secciones o método de corte (los 3 son el mismo).
Este video nos lo explica muy bien:
Si te ha gustado haz click en Compartir, Gracias:
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
TAMBIEN TE PUEDE INTERESAR
Estructuras Metalicas
Estructuras y Tipos de Estructuras
Puentes
Propiedades de los Materiales
Materiales de Construccion
Deformacion Elastica
Tipos de Soldadura
Proyectos de Estructuras
Soldadura Por Friccion
